Nullstellen quadratischer Funktionen
Inhaltsverzeichnis
\(\\\)
Quadratische Funktionen stellen als Graph eine Parabel dar.
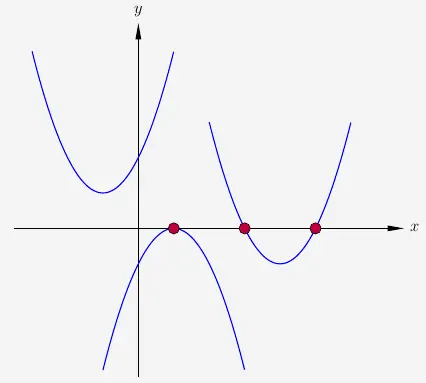
Wie wir hier sehen, kann eine quadratische Funktion eine, zwei oder auch keine Nullstellen haben.
\(\\[2em]\)
Lösungsansätze
In der allgemeinen Form, auch als Hauptform bezeichnet, liegt die quadratische Funktion als
\( \quad f(x) = ax^2 + bx + c \)
\(\\\)
vor.
Nicht immer sind alle Teile bei einer Funktionsgleichung vorhanden. Das wirkt sich auf die Berechnung der Nullstellen aus. Unterschiedliche Darstellungen erfordern es ein unterschiedliches Vorgehen.

\(\\\)
Wir betrachten das Ganze im Detail:
\(\\[1em]\)
Auflösen nach x
Liegt die Gleichung in der Form
\( \quad 0 = ax^2 + c \)
\(\\\)
vor, so können wir einfach nach \(x\) auflösen.
\( \quad \begin{array}{ r c l l l } 0 & = & 2x^2 - 18 & & | +18 \\[6pt] 18 & = & 2x^2 & & | :2 \\[6pt] 9 & = & x^2 & & | \sqrt{\dots} \\[6pt] x_1 & = & 3 & & \\[6pt] x_2 & = & -3 & & \\ \end{array} \)
\(\\\)

\(\\[2em]\)
Ausklammern mit dem Nullprodukt
Liegt die Gleichung in der Form
\( \quad 0 = ax^2 + bx \)
\(\\\)
vor, so verwenden wir nach den Lösungsansätzen das Ausklammern mit dem Nullprodukt.
\(\\[2em]\)
Regel vom Nullprodukt
Ist das Produkt \(a \cdot b = 0\) , so ist
\(\\\)
\(a = 0 \quad \textit{und/oder} \quad b = 0\).
\(\\\)
Wir gehen stets davon aus, dass beide Faktoren Null sind.
\(\\\)
Beispiel
\(\quad 0 = 3x^2 - 12x \)
\(\\\)
Es wird \(x\) ausgeklammert:
\( \quad 0 = x \cdot (3x - 12) \)
\(\\\)
Es werden nun folgende Fälle unterschieden:
\( \quad \begin{array}{ r c r c l l } \textrm{1. Fall: } & & x_1 & = 0 \\[24pt] \textrm{2. Fall: } & & 3x - 12 & = 0 & & | +12 \\[6pt] & & 3x & = 12& & | :3 \\[6pt] & & x_2 & = 4 \\ \end{array} \)
\(\\\)
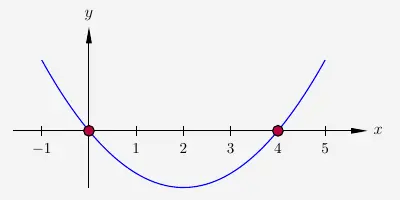
\(\\[2em]\)
PQ-Formel
Liegt die Gleichung in der Form
\( \quad 0 = ax^2 + bx + c \)
\(\\\)
vor, so verwenden wir nach den Lösungsansätzen die PQ-Formel:
\( \quad \boxed{ x_{1,2} = -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q} } \)
\(\\\)
Dabei ist zu berücksichtigen, dass man von der Normalform
\( \quad 0 = x^2 + px + q \)
\(\\\)
ausgeht. Der Parameter \(a\) ist also \(1\).
\(\\\)
Anmerkung:
\(\\\)
Wir unterscheiden hier zwischen der Hauptform mit \(a\)
\(f(x)=ax^2 + bx + c\)
\(\\\)
und der Normalform ohne \(a\)
\(f(x)=x^2 + px + q\) ,
\(\\\)
denn in vielen Fällen ist \(p\not=b\) und \(q\not=c\).
(Die Bezeichnungen Hauptform und Normalform werden in der Literatur nicht immer einheitlich verwendet.)
\(\\\)
Beispiel
\( \quad 0 = 3x^2 + 6x - 105 \)
\(\\\)
Zunächst bringen wird die Hauptform in die Normalform und beseitigen die \(3\) .
\( \quad \begin{array}{ r c l c l } 0 & = & 3x^2 + 6x - 105 & & | :3 \\[6pt] 0 & = & x^2 + 2x - 35 & & \\ \end{array} \)
\(\\\)
Hier ist \(p=2\) und \(q=-35\) . Eingesetzt in die PQ-Formel:
\( \quad \begin{array}{ r c l c l } x_{1,2} & = & -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q} \\[8pt] x_{1,2} & = & -\frac{2}{2}\pm \sqrt{\left(\frac{2}{2}\right)^2-(-35)} \\[8pt] x_{1,2} & = & -1\pm \sqrt{1^2 + 35} \\[8pt] x_{1,2} & = & -1\pm \sqrt{36} \\[8pt] x_{1,2} & = & -1\pm 6 \\[6pt] x_1 & = & -1 + 6 = -5 \\[6pt] x_2 & = & -1 - 6 = -7 \\ \end{array} \)
\(\\\)
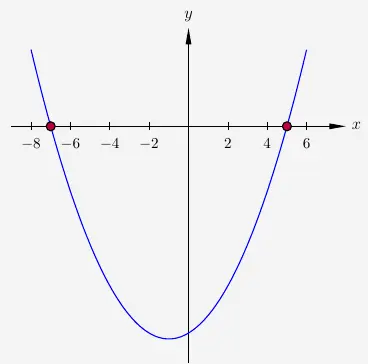
\(\\[2em]\)
Diskriminante
Den Ausdruck unter der Wurzel bei der PQ-Formel bezeichnet man als die Diskriminante \(D\).
\( \quad \begin{array}{ r c l } x_{1,2} & = & -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q} \\[6pt] x_{1,2} & = & -\frac{p}{2}\pm \sqrt{D} \\ \end{array} \)
\(\\\)
Die Diskriminante liefert Informationen über die Anzahl der Lösungen einer quadratischen Gleichung.
Es gilt:
\( \begin{array}{ r c l } D<0 & : & \text{keine reelle L}\ddot{o}\text{sung} \\[6pt] D=0 & : & 1 \text{ reelle L}\ddot{o}\text{sung} \\[6pt] D>0 & : & 2 \text{ reelle L}\ddot{o}\text{sungen} \\ \end{array} \)
\(\\\)
Es ist also durchaus möglich, keine Lösung zu erhalten. Wieso zeigt der Taschenrechner nun stets eine Lösung an? Dazu folgendes Beispiel:
\( \quad 0 = x^2 - 6x + 13 \)
\(\\\)
Die Funktion
\( \quad f(x) = x^2 - 6x + 13 \)
besitzt diesen Graphen:
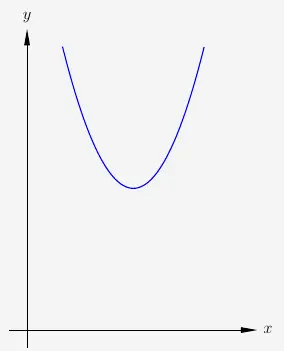
\(\\\)
Offensichtlich gibt es keine Nullstelle bei diesen Graphen. Rechnerisch ergibt die PQ-Formel
\( \quad \begin{array}{ r c l } x_{1,2} & = -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q} \\[8pt] x_{1,2} & = -\frac{-6}{2}\pm \sqrt{\left(\frac{-6}{2}\right)^2-13} \\[8pt] x_{1,2} & = 3 \pm \sqrt{(-3)^2 - 13} \\[8pt] x_{1,2} & = 3\pm \sqrt{-4} \\[6pt] x_1 & = 3 + \sqrt{-4} \\[6pt] x_2 & = 3 - \sqrt{-4} \\ \end{array} \)
\(\\\)
\(\sqrt{-4}\) liefert für \(x_1\) und \(x_2\) keine reelle Lösung, jedoch Lösungen aus den Bereich der komplexen Zahlen.
Die komplexen Zahlen bestehen aus einem reellen Anteil und einem imaginären Anteil. Der imaginäre Anteil enthält stets die imaginäre Zahl \(\mathbf{i}=\sqrt{-1}\).
Damit ergeben sich die Lösungen
\( \quad \begin{array}{ r c l } x_{1,2} & = & 3\pm \sqrt{-4} \\[6pt] x_{1,2} & = & 3\pm \sqrt{4 \cdot (-1)} \\[6pt] x_{1,2} & = & 3\pm \sqrt{4} \cdot \sqrt{-1} \\[6pt] x_{1,2} & = & 3\pm 2 \mathbf{i} \\[6pt] x_1 & = & 3 + 2 \mathbf{i} \\[6pt] x_2 & = & 3 - 2 \mathbf{i} \\ \end{array} \)
\(\\\)
Mit den komplexen Zahlen wird also der Zahlenbereich der reellen Zahlen erweitert, so dass nun folgende Zahlenmengen vorliegen:
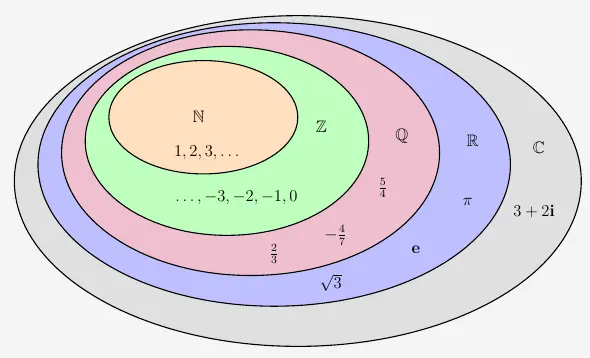
\(\\\)
Das Thema komplexe Zahlen wird an dieser Stelle nicht weiter vertieft, da es für die gymnasiale Oberstufe laut Lehrplan nicht vorgesehen ist. Zu einem späteren Zeitpunkt könnte es als gesondertes Thema behandelt werden.
\(\\[2em]\)
Satz des Viëta
Nach dem Satz des Viëta gilt
\( \quad 0 = x^2 + px + q = (x - x_1) \cdot (x - x_2) \)
\(\\\)
Daraus ergibt sich
\( \quad p = -(x_1+ x_2) \qquad und \qquad q = x_1 \cdot x_2 \)
\(\\\)
Beispiel
\( \quad 0 = x^2 + 5x + 6 \)
\(\\\)
\(x_1\) und \(x_2\) sind ganzzahlige (positive und negative) Teiler von \(q\). Infrage für die \(x\)-Werte kommen also Elemente aus der Menge
\( \quad \big\{-6, -3, -2, -1, 1, 2, 3, 6 \big\} \)
\(\\\)
Aufgestellt werden nun alle Multiplikationen, die \(6\) ergeben. Mit den Faktoren wird überprüft, ob sich daraus \(p=5\) bilden lässt.
\(\\\)
Mit \(x_1=-2\) und \(x_2=-3\) bekommen wir für \(p=5\) heraus. Also sind das die richtigen \(x\)-Werte.
\(\\\)
Aus dem Satz des Viëta resultiert die Linearfaktordarstellung einer ganzrationalen Funktion.
\(\\[1em]\)